 | History of the Chézy Formula |
 |
Antoine Chézy was born at Chalon-sur-Marne, France, on September 1, 1718, and died on October 4, 1798. He retired in 1790 under conditions of extreme poverty. It was not until 1797, a year before his death, that the efforts of one of his former students, Baron Riche de Prony, finally resulted in Chézy's belated appointment as director of the Ecole des Ponts et Chaussées.
In 1749, working in Amsterdam, Cornelius Velsen stated:
"The velocity should be proportional to the square root of the slope."
In 1757, in Hannover, Germany, Albert Brahms wrote:
"The decelerative action of the bed in uniform flow was not only equal to the accelerative action of gravity but also proportional to the square of the velocity."
They were working on the general laws and theories of Torricelli and Bernoulli. These are some of the main ideas that Chézy used to develop his formula. However, the credit goes to Chézy because his formula is not only the first but also the most lasting resistance formula.
Chézy was given the task to determine the cross section and the related discharge for a proposed canal on the river Yvette, which is close to Paris, but at a higher elevation. Since 1769, he was collecting experimental data from the canal of Courpalet and from the river Seine. His studies and conclusions are contained in a report to Mr. Perronet dated October 21, 1775. The original document, written in French, is titled "Thesis on the velocity of the flow in a given ditch," and it is signed by Mr. Chézy, General Inspector of des Ponts et Chaussées. It resides in file No. 847, Ms. 1915 of the collection of manuscripts in the library of the Ecole.
In 1776, Chézy wrote another paper, entitled: "Formula to find the uniform velocity that the water will have in a ditch or in a canal of which the slope is known." This document resides in the same file [No. 847, Ms. 1915]. It contains the famous Chézy formula:
v = 272 (ah/p)1/2in which h is the slope, a is the area, and p is the wetted perimeter. The coefficient 272 is given for the canal of Courpalet in an old system of units. In the metric system, the equivalent value is:
v = 31 (ah/p)1/2For the river Seine, the value of the coefficient is 44.
Herschel Clemens translated into English the two Chézy papers. He was the first person to translate the original documents into English in an accurate way. In the library of the Ecole, there is another document, without a date, but apparently written after 1775, which shows that Chézy had applied his formula on the flow in the pipe that conveyed water to the city of Rennes, France. In this case, the number 17 is the value given to the coefficient.
Current knowledge about Chézy's work is due to Girard and De Prony. Pierre-Simon Girard was chief engineer at Ponts et Chaussées and a member of the scientific mission to Egypt send by Napoleon Bonaparte. Baron Riche de Prony was one of Chézy's former students. De Prony was the first person to use the Chezy formula. Later, in 1801, in Germany, Eytelwein used both Chézy and De Prony's ideas to further the development of the formula. He gave the value of 50.9 [metric] to the coefficient.
sumber : http://chezy.sdsu.edu/
Chezy Equations Formulas CalculatorFluid Mechanics Open Channel Flow
Solving for flow velocity.
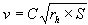
Inputs:
Conversions:
| Chezy coefficient (C) | = | 0 | = | 0 | ||
| hydraulic radius (rh) | = | 0 | = | 0 | meter | |
| slope (S) | = | 0 | = | 0 |
Solution:
| flow velocity (v) | = | HAS NOT BEEN CALCULATED |
Other Units:
Change Equation
Select an equation to solve for a different unknown
Chezy Equation
Chezy Coefficient
Select an equation to solve for a different unknown
Chezy Equation
| flow velocity | |
| Chezy coefficient | |
| hydraulic radius | |
| slope |
Chezy Coefficient
| Chezy coefficient | |
| roughness coefficient | |
| hydraulic radius |
References - Books:
Lindeburg, Michael R. 1992. Engineer In Training Reference Manual. Professional Publication, Inc. 8th Edition.
Lindeburg, Michael R. 1992. Engineer In Training Reference Manual. Professional Publication, Inc. 8th Edition.
sumber : http://www.ajdesigner.com/phpchezy/chezy_equation.php


Tidak ada komentar:
Posting Komentar